lemniscate

lemniscate

lemniscate [ lɛmniskat ] n. f.
• 1755; lat. lemniscatus, de lemniscus « ruban », d'o. gr., à cause de la forme en 8 d'une des lemniscates
♦ Math. Courbe correspondant au lieu géométrique des points tels que le produit de leurs distances à deux points fixes est constant.

● lemniscate nom féminin (latin lemniscatus, de lemniscus, ruban) Ovale de Cassini particulier, dont l'équation en coordonnées bipolaires est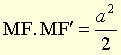 , pour 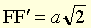. (Encore appelée lemniscate de Bernoulli, c'est une quartique, ayant le milieu de [FF′] pour point double.)

⇒LEMNISCATE, subst. fém.
GÉOM. Courbe en forme de huit et qui est le lieu géométrique des points tels que le produit de leurs distances à deux points fixes est constant. On voit immédiatement dans chacune de ces lames, les lemniscates produites par deux systèmes d'anneaux très-écartés; ces lemniscates sont tellement semblables, qu'il est à peu près impossible de dire si les axes sont plus écartés dans un sens que dans l'autre (DES CLOIZEAUX, Propr. opt. biréfringentes, 1857, p. 59). Pierrot avait repris sa course, décrivant avec élégance des lemniscates et des conchoïdes (QUENEAU, Pierrot, 1942, p. 28).
Prononc. : [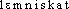]. Étymol. et Hist. 1755 (Encyclop. t. 5, s.v. ellipse). Empr. au lat. lemniscata, fém. de l'adj. lemniscatus « orné de lemnisques (lat. lemniscus, du gr. 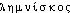désignant des rubans attachés aux couronnes, aux palmes des vainqueurs et des suppliants, ou ornant la tête des convives dans un festin) », lemnisque a été empr. au XVIe s., cf. GDF. Compl. et DG).

lemniscate [lɛmniskat] n. f.
ÉTYM. 1755, Encyclopédie; lat. lemniscatus « orné de bandelettes », de lemniscus « ruban », du grec lemniskôs (→ Lemnisque), à cause de la forme en 8 d'une des lemniscates.
❖
♦ Math. Courbe correspondant au lieu géométrique des points tels que le produit de leurs distances à deux points fixes est constant (→ Conchoïde, cit.).

Encyclopédie Universelle. 2012.

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Lemniscate — Lemniscate, eine schleifenförmige Kurve vierter Ordnung von der Gleichung (x2 + y2)2 = a2 (x2 – y2) oder in Polarkoordinaten Sie hat im Ursprung O einen Doppelpunkt mit Wendetangentenpaar. Die Punkte F und F a mit den Koordinaten… …   Lexikon der gesamten Technik

  • Lemniscate — (v. gr.), eine Curve des 4. Grades, deren Gleichung ist (x2 + y2)2 = 2a2 (x2 – y2); hierbei heißt a√2 die halbe Achse der L., daher man auch, indem man hiefür einen Buchstaben, z.B. b, einführt, die Gleichung so schreibt: (x2 + y2)2 + b2(y2 – x2) …   Pierer's Universal-Lexikon

  • Lemniscate — Une lemniscate est une courbe plane ayant la forme d un 8. Elle possède deux axes de symétrie perpendiculaires. Ceux ci se coupent en un point double de la courbe, également son centre de symétrie. Sommaire 1 Étymologie et histoire 2 Autres… …   Wikipédia en Français

  • Lemniscate — In algebraic geometry, the word lemniscate refers to any of several figure eight or ∞ shaped curves, of which the best known is the Lemniscate of Bernoulli. It is also sometimes used to refer to the infty symbol used in mathematics as a symbol… …   Wikipedia

  • Lemniscate — Lemniscata Lem nis*ca ta (l[e^]m n[i^]s*k[=a] t[.a]), Lemniscate Lem*nis cate (l[e^]m*n[i^]s k[asl]t), n. [L. lemniscatus adorned with ribbons, fr. lemniscus a ribbon hanging down, Gr. lhmni skos.] (Geom.) A curve in the form of the figure 8,… …   The Collaborative International Dictionary of English

  • lemniscate — /lem nis kit, lem nis kayt , kit/, n. Analyt. Geom. a plane curve generated by the locus of the point at which a variable tangent to a rectangular hyperbola intersects a perpendicular from the center to the tangent. Equation: r2=2a2cos(t). Also… …   Universalium

  • Lemniscate De Bernoulli — La lemniscate de Bernoulli. La lemniscate de Bernoulli est une courbe plane. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli. Une lemniscate de Bernoulli, de foyers F et F’, est l ensemble des points M vérifiant la… …   Wikipédia en Français

  • Lemniscate de bernoulli — La lemniscate de Bernoulli. La lemniscate de Bernoulli est une courbe plane. Elle porte le nom du mathématicien et physicien suisse Jacques Bernoulli. Une lemniscate de Bernoulli, de foyers F et F’, est l ensemble des points M vérifiant la… …   Wikipédia en Français

  • Lemniscate De Booth — Lemniscates de Booth, pour différentes valeurs de c. c = 0,25 (noir) c = 0,5 (rouge) c = 0,75 (vert) c = 1 (bleu). En géométrie algébrique, la lemniscate de Booth, aussi appelée courbe de Booth, ovale de Booth ou encore hippopède de Proclus, est… …   Wikipédia en Français

  • Lemniscate de booth — Lemniscates de Booth, pour différentes valeurs de c. c = 0,25 (noir) c = 0,5 (rouge) c = 0,75 (vert) c = 1 (bleu). En géométrie algébrique, la lemniscate de Booth, aussi appelée courbe de Booth, ovale de Booth ou encore hippopède de Proclus, est… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”